11058. Погоня за бабочкой
В ясные летние дни Нюша любит
ловить бабочек на свежем воздухе. Но сегодня ей попалась особенно хитрая
бабочка: она залетела в лабиринт и попыталась скрыться там от Нюши.
Лабиринт состоит из n
комнат, пронумерованных от 1 до n, некоторые из которых соединены
коридорами. Известно, что между любыми двумя комнатами существует единственный
путь, проходящий только по коридорам. Иными словами, лабиринт представляет
собой дерево, состоящее из n вершин и n − 1 рёбер.
Вход в лабиринт находится в
комнате с номером 1. Листом называется любая комната, соединённая ровно с одной
другой комнатой и не совпадающая с корнем (комнатой номер 1). В каждом листе
расположен выход из лабиринта. Бабочка начинает свой полёт из комнаты номер 1 в
направлении одного из выходов. Она движется с постоянной скоростью, не
разворачивается, и каждую минуту пролетает один коридор, переходя в соседнюю
комнату. Все коридоры имеют одинаковую длину.
Чтобы поймать бабочку, Нюша
решила позвать на помощь несколько друзей. Изначально каждый из них может
занять любую из комнат с выходом. Как только бабочка начнёт движение от входа к
какому-либо выходу, друзья могут сразу же начать двигаться из своих комнат по
направлению ко входу. Они двигаются с той же скоростью, что и бабочка. Если
кто-либо из них встретит бабочку – будь то в комнате или на середине коридора –
она считается пойманной. Если же бабочка доберётся до выхода, не столкнувшись
ни с одним из друзей, она благополучно выберется на свободу.
Помогите Нюше определить
минимальное число друзей, необходимое для того, чтобы гарантированно поймать
бабочку, вне зависимости от того, к какому выходу она полетит.
Вход. Первая строка содержит одно целое число n (2 ≤ n ≤ 200000) – количество комнат в лабиринте.
Следующие n – 1 строк
описывают коридоры, соединяющие комнаты. В каждой из них записаны два целых
числа u и v (1 ≤ u, v ≤ n, u
≠ v) – номера комнат, соединённых коридором.
Гарантируется, что заданная
система коридоров образует дерево.
Выход. Выведите одно целое число – минимальное количество друзей, необходимое для того, чтобы гарантированно поймать
бабочку.
|
Пример
входа 1 |
Пример
выхода 1 |
|
3 1 2 1 3 |
2 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
4 1 2 2 3 2 4 |
1 |
РЕШЕНИЕ
графы –
поиск в глубину
Анализ
алгоритма
Выполним
обход в глубину из вершины 1. Для каждой вершины вычислим два значения:
·
d[v] – расстояние от вершины 1 до вершины v.
Если p – родитель v, то
d[v]
= d[p] + 1
·
h[v] – расстояние от вершины v до ближайшего листа в поддереве с корнем v.
Если to1,
to2, …, tok – сыновья вершины v, то
h[v]
= 1 + min(h[to1], h[to2], …, h[tok])
·
Если v
– лист дерева, то положим h[v]
= 0.
Затем
запустим второй обход в глубину. В ходе этого обхода будем вычислять значение res[v] – минимальное количество друзей,
которых нужно разместить в некоторых из листьев поддерева с корнем в вершине v,
чтобы гарантированно поймать бабочку, при условии, что она выбрала это
поддерево.
Если h[v] ≤ d[v], то res[v] = 1. В этом случае достаточно разместить одного друга в листе с минимальной глубиной в
поддереве вершины v: он успеет дойти до вершины v не позже, чем
бабочка — из корня дерева.
В
противном случае, если to1,
to2, …, tok – сыновья вершины v, то
res[v]
= res[to1] + res[to2] + … + res[tok]
Если
бабочка не будет поймана в самой вершине v, необходимо быть готовыми
перехватить её в любом из поддеревьев, исходящих из сыновей v.
Искомым
ответом на задачу является значение res[1].
Пример
В
первом примере (на рисунке слева) требуются два друга, которых необходимо
разместить у двух выходов. Бабочка может полететь из вершины 1 либо в вершину
2, либо в вершину 3. В любом из этих случаев её перехватит один из друзей Нюши.
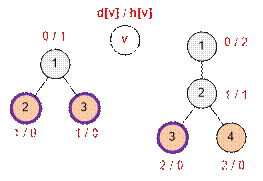
Во
втором примере (на рисунке справа) достаточно одного друга, которого можно
разместить в любом из двух выходов – вершине
3 или 4. За одну минуту бабочка долетит из вершины 1 до вершины 2. За это же
время друг доберётся до вершины 2 и поймает бабочку там.
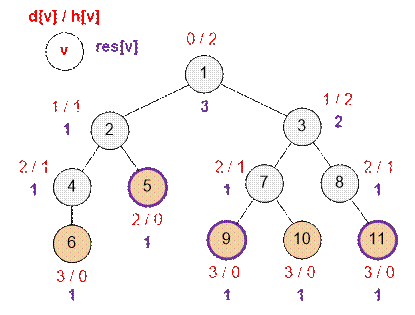
Рассмотрим следующий пример.
Для поимки бабочки Нюше понадобятся
три друга.
Реализация алгоритма
Объявим константу бесконечность и
рабочие массивы.
#define INF 2000000000
vector<vector<int>
> g;
vector<int> d, h, res;
Функция
dfs (v, p, cnt) выполняет обход в глубину,
начиная с вершины v, и возвращает значение h[v]. При этом p
– предок вершины v, а cnt – расстояние от вершины 1 до v.
В процессе обхода для каждой вершины v вычисляются значения d[v]
и h[v].
int dfs(int v, int p = -1, int cnt = 0)
{
Значение
cnt, равное расстоянию от вершины 1 до v, сохраняем в d[v].
d[v] = cnt;
int height = INF;
Перебираем всех сыновей вершины v.
Рассматриваем ребро v → to. Если to совпадает с предком v (to = p),
переходим к следующему сыну.
for (int to : g[v])
if (to !=
p)
В переменной height
вычисляем значение
min(h[to1],
h[to2], …, h[tok]),
где to1,
to2, …, tok – сыновья вершины v.
height = min(height, dfs(to, v, cnt + 1));
Если height = INF, значит вершина v
является листом, и следует установить h[v] = 0. В противном случае возвращаем
h[v]
= 1 + min(h[to1], h[to2], …, h[tok])
return h[v] =
(height == INF) ? 0 : 1 + height;
}
Функция
dfs2 (v, p) выполняет обход в глубину, начиная с
вершины v, и возвращает значение res[v].
Здесь p – предок вершины v.
int dfs2(int v, int p = -1)
{
int s = 0;
Пусть to1,
to2, …, tok – сыновья вершины v. В переменной s
вычислим сумму:
res[to1]
+ res[to2] + … + res[tok]
if (to !=
p)
{
dfs2(to, v);
s +=
res[to];
}
Если h[v] ≤ d[v], то достаточно одного друга, и res[v] = 1. Иначе
res[v]
= res[to1] + res[to2] + … + res[tok] = s
return res[v] = (h[v] <=
d[v]) ? 1 : s;
}
Основная
часть программы. Читаем входные данные. Строим граф.
scanf("%d", &n);
g.resize(n + 1);
for (i = 0; i < n - 1; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
Инициализируем
массивы.
d.resize(n + 1);
h.resize(n + 1);
res.resize(n + 1);
Запускаем
два обхода в глубину. Первый обход для каждой вершины v вычисляет
значения d[v] и h[v].
dfs(1);
dfs2(1);
Выводим
ответ – минимальное количество друзей, необходимое
для поимки бабочки.
printf("%lld\n", res[1]);